Positive Beispiele zu negativen Zahlen Mathias Hattermann ist neuer Professor für Mathematikdidaktik

Den Mathematik-Studierenden des Lehramtes den Studienanfang zu erleichtern, liegt Mathias Hattermann besonders am Herzen. Als neuer Professor für Mathematikdidaktik möchte er der Studieneingangsphase mehr Aufmerksamkeit widmen. Wie digitale Medien beim Mathematiklernen unterstützen können, wie man Schülerinnen und Schüler für den Mathe-Unterricht begeistern kann, was positive Beispiele für negative Zahlen sind und warum Mathe ein tolles Fach ist, hat er Bianca Loschinsky im Interview erzählt.

Herr Hattermann, Sie sind seit 1. Oktober neuer Professor für Mathematikdidaktik für die Sekundarstufen I und II im Institut für Didaktik der Mathematik und Elementarmathematik. Sind Sie gut an der TU Braunschweig angekommen?

Meine Kolleginnen und Kollegen haben mich hier in Braunschweig sehr nett empfangen und mir jegliche Unterstützung angeboten und gegeben, die man sich nur wünschen kann. Die Einarbeitung in die ungewohnten Systeme und Abläufe ist bisweilen noch etwas holprig, aber in Anbetracht der kurzen Zeit fühle ich mich sehr gut integriert, zumindest was die universitären Abläufe betrifft.

Warum haben Sie sich für die Carolo-Wilhelmina entschieden?

Als technische Universität bringt die TU Braunschweig meinem Fach sozusagen „von Natur aus“ einen gewissen Respekt entgegen, was mir natürlich gefällt. Zudem wird in Braunschweig Spitzenforschung betrieben. Darüber hinaus sind auch die Aktivitäten am Institut für Didaktik der Mathematik und Elementarmathematik in wissenschaftlicher Hinsicht vielfältig und international angebunden, sodass ich hier ein attraktives Arbeitsumfeld vorfinde, in das ich mich in den kommenden Monaten einbringen werde.

Sie haben zuletzt an der Universität Paderborn gearbeitet und sich dort unter anderem mit „positiven Beispielen zu negativen Zahlen“ beschäftigt. Um was geht es dabei?

Hierbei handelt es sich um die Weiterführung eines Forschungs-und-Entwicklungsprojektes, das ich zusammen mit der Uni Bielefeld und der wissenschaftlichen Leitung der Laborschule in Bielefeld durchgeführt habe. Dabei geht es um einen handlungsorientierten Zugang zur Addition und Subtraktion ganzer Zahlen, insbesondere um Rechnungen der Form -4 – (-12) = . Ziel der Unterrichtsreihe war, Konzepte zu entwickeln, die Schülerinnen und Schülern helfen, mathematische Konzepte mit konkreten Situationen zu verbinden, um diese kognitiv besser verarbeiten zu können. Aktuell denken wir über eine Fortführung des Projektes nach und führen bereits Gespräche, um einen Forschungsantrag auf den Weg zu bringen.

Was wäre denn ein positives Beispiel für negative Zahlen, indem ein mathematisches Konzept mit einer konkreten Situation verbunden wird?

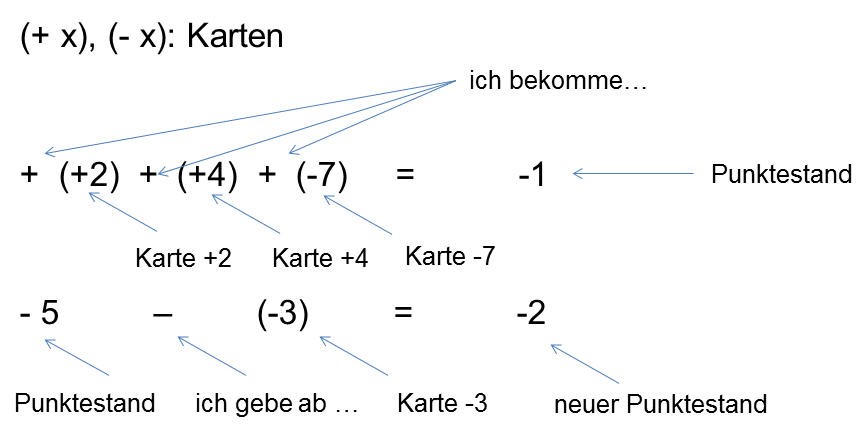
Wir haben hierzu ein Kartenspiel genutzt, um die unterschiedliche Bedeutung von Rechenzeichen und Vorzeichen sowie die erforderliche Klammersetzung, die beide für Schülerinnen und Schüler bisweilen schwierig sind, zu erklären. Hierzu wurde ein abwechslungsreiches Spiel mit entsprechenden Spielregeln konzipiert: Dabei dienten das Aufnehmen und Abgeben bzw. die Bezeichnung der Spielkarten selbst, zum Beispiel die Karte (-7), dazu, die beiden mathematischen Konzepte Rechen- und Vorzeichen auch auf der inhaltlichen Ebene des Spiels voneinander zu trennen. Das Erhalten bzw. das Abgeben von Karten wurde mit den Rechenzeichen + bzw. – verbunden, während die Verwendung der entsprechenden Vorzeichen (ebenfalls + und -) zur Bezeichnung der Karten selbst diente. Dies erleichterte den Schülerinnen und Schülern das Rechnen, da sie die entsprechenden Aufgaben mit konkreten und selbst erlebten Spielsituationen verbinden konnten.

Auch das Setzen von Klammern konnte so erklärt werden, dass Karten mit Klammern geschrieben werden müssen, während Punktestände ohne Klammern zu notieren waren.  Aus mathematischer Sicht dürfen Rechen- und Vorzeichen nicht direkt „aufeinandertreffen“. In den Untersuchungen zeigte sich, dass damit fast alle Schülerinnen und Schüler bekannte Schwierigkeiten beim Umgang mit ganzen Zahlen überwinden konnten.

Mit welchen Forschungsschwerpunkten und Projekten werden Sie sich an der TU Braunschweig auseinandersetzen?

Ein Schwerpunkt meiner Arbeit wird sich weiterhin mit digitalen Medien und deren Umsetzung und Wirkung in Schule und Hochschule beschäftigen. Gerade die Übergangsproblematik Schule-Hochschule liegt mir hierbei besonders am Herzen. Deshalb arbeite ich auch sehr gerne mit Studierenden in der Studieneingangsphase. Die Hochschulmathematik unterscheidet sich deutlich von der Schulmathematik und das macht den Studienbeginn für viele schwer. Jedoch bin ich der Überzeugung, dass man mit etwas Geduld und Zeit nicht allen, aber sehr vielen Studierenden den Studienanfang erleichtern kann. Dies kann dadurch gelingen, dass man der Studieneingangsphase mehr Aufmerksamkeit widmet, dort das Tempo in der Lehre verringert und die neuen Methoden und Konzepte anhand einfacher schulnaher Inhalte behandelt.

Welche Rolle spielt die Digitalisierung im künftigen Mathe-Unterricht? Wie können digitale Medien beim Mathematiklernen unterstützen?

Aus meiner Sicht ist das Potenzial von digitalen Medien für den allgemeinen Unterricht immens und hinsichtlich der Tragweite momentan kaum abzuschätzen. Der Unterricht und insbesondere der Mathematikunterricht werden sich verändern, sie werden kooperativer, vernetzter, abwechslungsreicher und für manche auch attraktiver. Um dieses Potenzial ausschöpfen zu können, benötigen wir jedoch die entsprechenden Konzepte und Lehrerinnen und Lehrer, die diese umsetzen können. Uns nützen keine Tablets in den Schulen, die lediglich zum Abrufen von E-Mails genutzt werden. Verabschieden sollten wir uns jedoch von der Vorstellung, dass die digitalen Medien uns von der geistigen Anstrengung beim Verstehen von Mathematik befreien und das ist auch gut so.

Mathe ist nicht immer das Lieblingsfach von Schülerinnen und Schülern. Wie kann man sie für das Fach begeistern? Wie sollte der Mathe-Unterricht der Zukunft aussehen?

Mathematik ist ein tolles Fach, das flexibel von der Lösung einfacher Alltagsaufgaben über komplexere Problemlösekompetenzen bis hin zu großen intellektuellen Herausforderungen einsetzbar ist. Es müsste also eigentlich für jeden Geschmack etwas dabei sein. Im Mathematik-Unterricht hat sich auch schon sehr viel getan, nichtsdestotrotz haben wir Didaktikerinnen und Didaktiker noch viel zu tun. Das Hauptproblem bei der Vermittlung von Mathematik in der Schule ist aus meiner Sicht immer noch, dass die Mathematik bisweilen als technisches Regelwerk unterrichtet wird, dessen Durchführung eingeübt werden muss. Aber Mathematik ist viel mehr als Rechengesetze und Algorithmen und das müssen wir unseren Schülerinnen und Schülern vermitteln. Mathematik ist ausprobieren, vermuten, erkunden, irren, nach Bestätigung suchen, begründen, beweisen, erklären, sich anstrengen, verstehen, scheitern, lösen, kooperieren, sich gegenseitig unterstützen … Und unsere Schülerinnen und Schüler müssen die Chance haben, diese Bandbreite auch im Regelunterricht zu erfahren, um ein authentisches Bild von Mathematik gewinnen zu können.

Was begeistert Sie selbst an der Mathematik?

Ein Fachmathematiker aus Paderborn hat mal gesagt, dass es ein schönes Gefühl sei, etwas verstanden zu haben und dem pflichte ich bei. Beim mathematischen Arbeiten hat man auf wirklich allen Anforderungsniveaus von der Grundschule bis zur Hochschule andauernd die Chance bzw. die Herausforderung etwas zu verstehen. Wenn man diese Hürde nimmt, ist dies in der Tat ein sehr schönes und befriedigendes Gefühl. Die Mathematik ist aus universitärer Sicht betrachtet ein logisches Gebäude, dessen Entstehung man von den kleinsten Bausteinen an genau verfolgen kann und das macht sie einzigartig, da man ihre Erkenntnisse beweisen kann und diese auch in 100.000 Jahren und darüber hinaus Bestand haben werden.

Seit der Corona-Pandemie hat sich das Lehren und Forschen an den Universitäten verändert. Welche besonderen Herausforderungen sehen Sie im Wintersemester?

Ich habe ein bisschen Sorge, was unsere Studierenden in den ersten Semestern betrifft. Für Studienanfängerinnen und -anfänger ist es besonders wichtig, sich in Lerngruppen zu treffen, möglichst viel über Mathematik zu sprechen, Erfahrungen zu teilen und gemeinsam „am Ball“ zu bleiben. Dies alles wird durch die Regeln zur Eindämmung der Corona-Pandemie erschwert, weswegen diese Studierendengruppe besondere Aufmerksamkeit benötigt. Da ich selbst eine Veranstaltung für Erstsemester halte, bin ich gespannt, wie unsere digitalen Konzepte angenommen werden und wie die Studierenden selbst ihr erstes digitales Semester beurteilen.

Was möchten Sie den Studierenden mit auf den Weg geben?

Seien Sie immer neugierig, scheuen Sie sich nicht Fragen zu stellen, geben Sie nicht auf und bleiben Sie am Ball. Versuchen Sie die Mathematik als intellektuelle Herausforderung zu betrachten, die Sie mit einem gewissen Einsatz und der erforderlichen Hartnäckigkeit sowie Ausdauer bewältigen werden.